As a first check of the moving boundary model, a monochromatic wave train is let to runup and rundown a plane beach. The model is compared with the analytic solution derived by Carrier and Greenspan (1958) for monochromatic long wave runup on a constant slope. Their derivation makes use of the non-linear shallow water equations, and thus for consistency the dispersive terms will be ignored in the numerical simulations for this comparison.
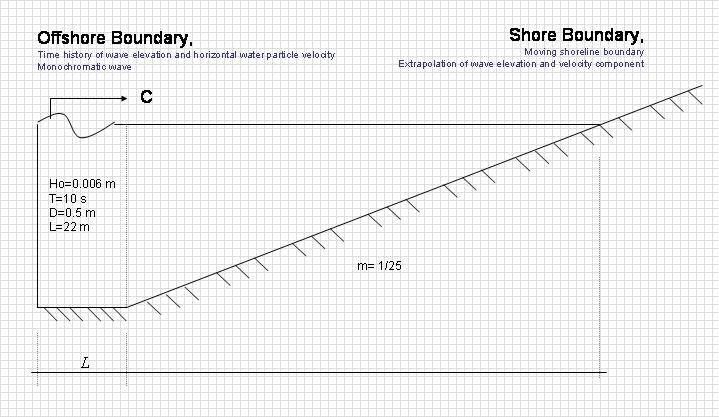
Simulation of non-breaking regular wave runup propagation on a sloping beach is shown below
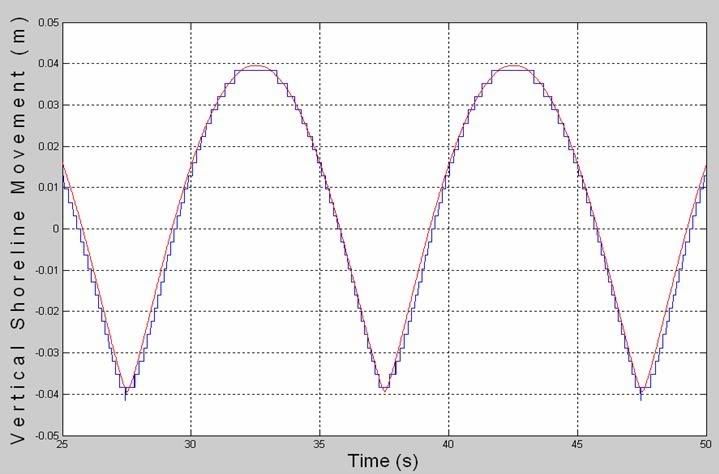
Figure below shows a comparison between analytical (Carrier and Greenspan, 1958) and numerical solution of vertical shoreline movement. The analytic solution is indicated by a red line while the numerical solution is indicated by a blue line. It is concluded that non-breaking regular wave runup is accurately predicted by the proposed model, yielding a validation of the moving boundary technique.
Simulation of Non-breaking Regular Wave Propagation on a Constant Depth
Simulation of Non-breaking Regular Wave Propagation on a Sloping Beach up to Breaking Location
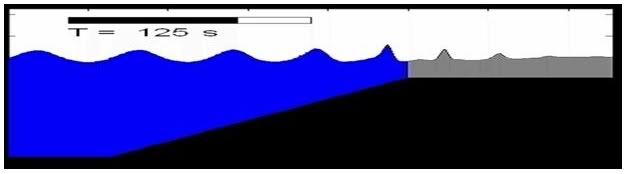
Simulation of Breaking Regular Wave Propagation on a Sloping Beach up to Very Shallow Water Depth
Simulation of Breaking Regular Wave Runup Propagation on a Sloping Beach