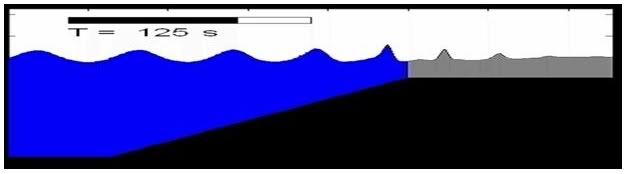
Simulation of breaking regular wave propagation on a sloping beach up to very shallow water is computed in order to test wave breaking model. Figure below shows numerical experiment setup where initial wave properties and bathymetry condition are described. At the left boundary, time history of wave elevation and horizontal water particle velocity based on 5th order Stokes wave are applied.
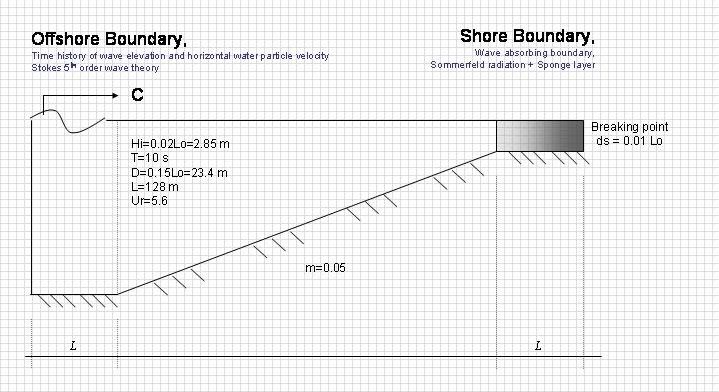
In simulation below wave transformation increasing in their wave heights during propagate to shore are well simulated. With further decrease in water depth an asymmetrical wave profile are also clearly observed and once the wave exceed breaking location, their height is decreasing due to energy dissipation.
Although there is a reflected wave due to introduction of discontinuity of dissipation breaking term, comparison between numerical and analytical solution show fairly good agreement. The analytic solution is indicated by a red line while the numerical solution is indicated by a blue dotted-line.
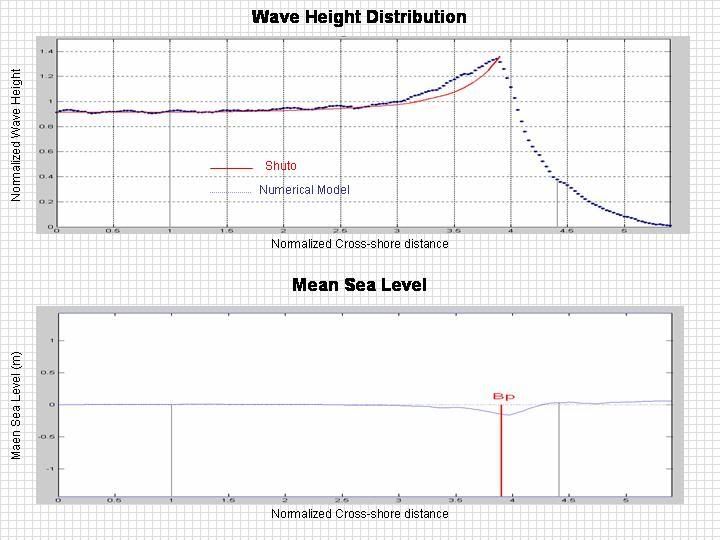
Secondary effects like wave setdown seaward of the breaker and wave setup landward of the breaker are also clearly indicated. The minimum mean sea water level is about 5 % of wave height at the breaking location which is also inline with nonlinear properties derived from conservation equation.
Simulation of Non-breaking Regular Wave Propagation on a Constant Depth
Simulation of Non-breaking Regular Wave Propagation on a Sloping Beach up to Breaking Location
Simulation of Non-breaking Regular Wave Runup Propagation on a Sloping Beach
Simulation of Breaking Regular Wave Runup Propagation on a Sloping Beach