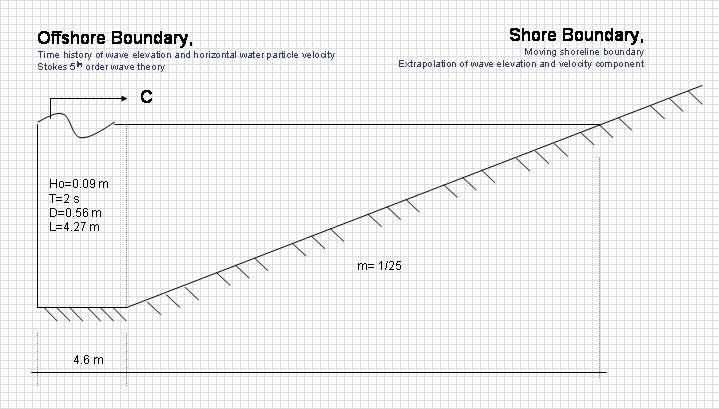
Simulation of breaking regular wave runup propagation on a sloping beach is computed in order to test both wave breaking model and wave runup simultaneously. Figure below shows numerical experiment setup where initial wave properties and bathymetry condition are described. At the left boundary, time history of wave elevation and horizontal water particle velocity based on 5th order Stokes wave are applied. At the right boundary, moving shoreline boundary employ a linear extrapolation of free surface displacement and velocity components, are applied.
The numerical model was initially evaluated using data obtained from experiments carried out by Nwogu (1993) in the three-dimensional wave basin of the Canadian Hydraulics Center.
It would seem that inclusion of an accurate dissipation term becomes increasingly important with increasing degree of wave breaking. Introduction of a bottom friction alone as a dissipation term in a very small total water depth may create an equally large dissipative momentum flux, which can lead to an overflow in the iterative numerical scheme due to the fact that bottom friction term is inversely proportional to the total water depth. This statement is not restricted to simulations that contain a shoreline, any simulation with periodic wave breaking suffers from this difficulty.

The other reason is that as the wave propagates to shore the wave face becomes too steep and it creates instability during extrapolation of water surface in wave runup model. In regard to breaking regular wave runup simulation additional dissipation term was required for long term stability.
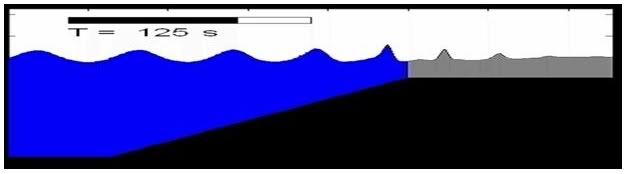
Simulation shows the propagation breaking regular wave runup on a sloping beach. With further decrease in water depth an asymmetrical wave profile are also clearly observed and once the wave exceed breaking location, their height is decreasing due to energy dissipation.
Figure below shows the wave height distribution and mean sea water level obtained by the model and measurements. The overall agreement is seen to be fairly good but there some discrepancies: wave height is slightly underestimated around the breaking point and the calculated wave setup is also underestimated.

Simulation of Non-breaking Regular Wave Propagation on a Constant Depth
Simulation of Non-breaking Regular Wave Propagation on a Sloping Beach up to Breaking Location
Simulation of Breaking Regular Wave Propagation on a Sloping Beach up to Very Shallow Water Depth
Simulation of Non-breaking Regular Wave Runup Propagation on a Sloping Beach