Coastal zone is one of the most valuable regions on earth from the viewpoint of the ecosystem and human welfare. The coastal zone has been recognized as natural resources for the activities of human beings and has been utilized for various purposes. Coastal zone has also an important ecological value due to plenty of diversity in habitats.
These days the protection of coastal areas has become one of the more pressing environmental problems in many countries. Most of these problems are related to the wave and current phenomena in the nearshore zone. These phenomena have thus attracted immensely the interest of engineers in order to safeguard multi-faceted activities in the coastal zone.
Understanding nearshore waves has become an indispensable tool in the estimation of forces for the proper design and construction of coastal infrastructures. Waves attack coastal structure and infiltrate harbor entrance, generating disturbance in the sheltered waters. Hence, it is also necessary to know beforehand the magnitude and direction of propagating waves to design the optimal layout of harbors.
As waves propagate toward shore, a combination of shoaling, refraction, reflection, diffraction, and breaking effects modify the waveform, and the wave characteristics will be very different from those in deep water. The ability to accurately predict wave transformation from deep to shallow water is vital to an understanding of coastal processes. By the refraction the directions of wave propagation as well as the wave height vary in accordance with the sea bottom topography. By the wave shoaling the wave height gradually change as a result of the change of the rate of energy flux due to the reduction in water depth, even if no refraction takes place.
When incoming waves are interrupted by a barrier such as a breakwater or an island, the waves curve around the barrier and penetrate into the sheltered area, this phenomenon is called diffraction. When waves reach a water of depth less than a few times the wave height, waves begin to break and the overall wave height decreases as the wave energy is dissipated.
The processes of wave breaking, runup, setdown and setup of the mean water level, turbulent energy production, generation of nearshore currents and generation of infragravity waves are important driving mechanisms for the transport of sediments and pollutants as well as erosions in coastal regions.
Most coastal erosion and accretion problems can be prevented or mitigated with some engineering knowledge of coastal sedimentation. Periodic dredging operation and channel navigation can be planned and managed more precisely and effectively. The understanding of effects caused by existing or newly constructed coastal structure is also some of the benefits derived from a detailed modeling of the wave and current phenomena in shallow water.
The effects of man-made or naturally caused changes around coastal area can be examined through physical modeling. This usually involves intricate and time consuming setting up of a scaled-down physical model and requires accurate measurements of wave data. With the availability of advanced computing facilities, numerical model has become an attractive alternative. The shift towards numerical modeling has resulted in rapid developments of numerical methods for solving water wave equations.
The greatest advance of numerical model over a physical model is its ability to determine the required information at a much shorter period with a comparatively larger degree of accuracy. The same numerical model may also be used repeatedly on different problems with only some minor modification in boundary conditions, bathymetry and incident wave condition.
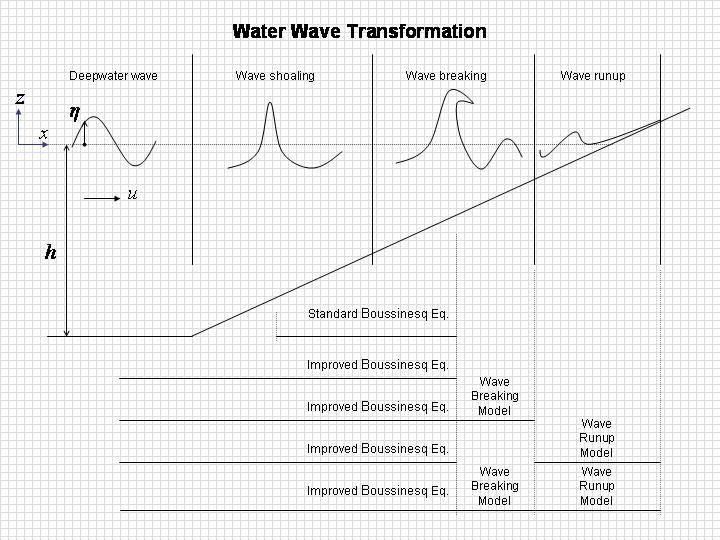
It has long been a goal of coastal engineers to produce a computational wave model that is capable of accurately simulating wave motion from deep water through the surf zone. To do this, a model would have to include, among other things, nonlinear shoaling, refraction, diffraction, wave-wave interaction, breaking, and runup.
Early numerical model, owing perhaps to limitations in computing capability, were mostly based on the Airy (1845) linear wave theory wherein the pressure distribution in the vertical is assumed to be hydrostatic.
In the nearshore region, where water depth and shallow and amplitude may still be large, wave is highly nonlinear, characterized by asymmetric orbital motion of the water particle. The nonlinearity becomes increasingly dominant with decreasing water depth. Hence, it may be expected that numerical models based on the linear wave theory will not provide an accurate simulation of the nearshore wave phenomenon.
Linear theory also cannot simulate the secondary effects of the wave action such wave set-up and wave set-down. Nonlinear wave theories include the wave nonlinearities and simulate simultaneously the wave phenomenom and its secondary effects.
The mathematical description on nonlinear water wave involves the Laplace equation combined with nonlinear boundary conditions at the free-surface and at the sea bottom. This problem is complicated by the fact that the moving surface boundary is part of the solution. Direct numerical methods for solving the full equations exist but they are extremely time consuming and can only be applied to small scale problems. As it is currently impractical to perform a full solution over any significant domain, approximate models must be used. For this reason there is a strong interest in so-called Boussinesq-type formulations of the water wave problem.
The principle behind Boussinesq formulations is to incorporate the effects of non-hydrostatic pressure, while eliminating the vertical coordinate, thus significantly reducing the computational effort relative to a full three-dimensional solution. This principle was initially introduced by Boussinesq (1872), who derived new governing equations under the assumption that the magnitude of the vertical velocity increases polynomially from the bottom to the free surface which inevitably leads to some form of depth limitation in the accuracy of the embedded dispersive and nonlinear properties. Hence, Boussinesq-type equations are conventionally associated with relatively shallow water.
Due to increasing error in the modeled linear dispersion relation with increasing water depth, the standard Boussinesq equations are limited to relatively shallow water. Recently, efforts were made by a number of investigators to derive alternative forms of Boussinesq equations that can be applied in deeper water regions. In order to make the Boussinesq equations applicable in deeper water, many researchers have suggested the ways to extend the validity range of the equations. The extended Boussinesq equations normally have adjustable polynomial approximations for the exact dispersion relationship, a major improvement from the standard ones.
Recent developments in numerical schemes for solving Boussinesq-type equation have placed immense interest in nonlinear dispersive wave models based on the Boussinesq equations. One set of candidate models is the various Boussinesq-type equations (Peregrine 1967; Madsen and Sørensen 1992; Nwogu 1993; Wei et al. 1995). These can describe, to varying degrees of accuracy in representing nonlinearity and dispersion, most phenomena exhibited by non-breaking waves in finite depths.
However, as derived, they do not include dissipation due to wave breaking and thus become invalid in the surf zone. Therefore, it is necessary to implement the proper wave breaking model to the well developed Boussinesq wave model for simulating the surf zone phenomena in nearshore zone.
Although all of these efforts extend the usage of the Boussinesq-type equation model such that wave evolution from relatively deep water to the breaking point could be accurately captured, but the process of runup and rundown is not. There has been only limited success developing a general model which can theoretically predict the runup of arbitrary wave especially the wave break during approach to the shoreline. Even non-breaking waves are difficult to treat because the shoreline represents a moving boundary, which must be computed as part of the solution.
Objectives of the Study
The main objective of this study is to develop high-order numerical scheme that can be used to solve the improved nonlinear dispersive one-dimensional Boussinesq equations. This scheme has ability to accurately predict wave transformation from deep to shallow water and to simulate most of the phenomena of interest in the nearshore zone.
The numerical model based on these equations is also extended to simulate one-dimensional wave propagation in the shallow water region over a horizontal or mildly sloping bed to include wave transformation inside the surf zone.
A one-dimensional wave breaking criterion is used to determine the location of the breaking point. With the determination of the breaking point, by choosing a proper wave breaking model and implement it in the developed wave model, simulation of the surf zone wave transformation as well as secondary effects like wave set-down and wave set-up are also simulated.
Finally, a moving boundary technique utilizes linear extrapolation is developed to investigate wave runup and rundown. The moving boundary is tested for accuracy using one-dimensional analytical solutions.
References can be found here.