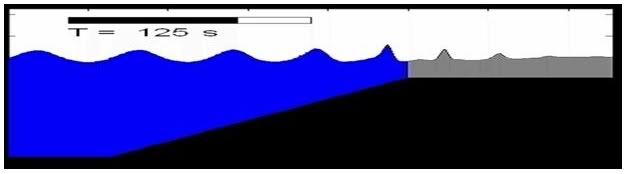
A finite-difference numerical scheme that solves Nwogu’s one-dimensional Boussinesq equation on a staggered-grid system is presented. A staggered grid system is introduced with the first-order spatial derivatives being discretized by the fourth-order accurate finite-difference scheme. For the time derivatives, the fourth-order accurate Adams predictor–corrector method is used. As a result, both the numerical dissipation and dispersion are kept into higher-order.
The new form of one-dimensional Boussinesq equations derived by Nwogu (1993) are given by

These equations are statements of conservation of mass and momentum, respectively. Compared to the Boussinesq equations based on depth-averaged velocity (referred to hereafter as standard Boussinesq equations) derived by Peregrine (1967), there is an additional dispersive term in continuity equation and the coefficients of dispersive terms in the momentum equations are different.
The governing equations are finite-differenced on a staggered grid system.
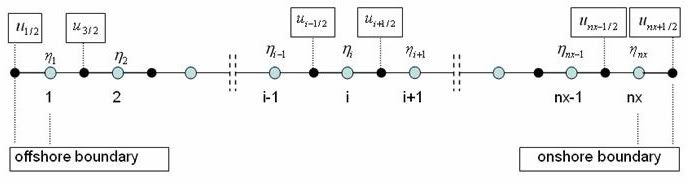
First order derivatives of wave elevation employ the fourth-order accurate four-point central difference scheme. Advective term of wave velocity employs the second-order upwind scheme. Dispersive terms employ the second-order accurate three-point central difference scheme.

Discretization in time step of the governing equation consists of the third-order Adams-Bashforth predictor and fourth-order Adams-Moulton corrector schemes.

Boundary Condition
Appropriate boundary conditions are needed for the numerical model to run properly. The examples shown in the following involve two types of boundaries: incident wave boundary (offshore boundary) and absorbing boundary (onshore boundary).
Incident wave boundary (offshore boundary)
In offshore boundary the time series of incident wave elevation and the horizontal velocities are imposed and can be directly obtained from finite amplitude stokes or cnoidal waves theory. In Stokes wave theory, the wave steepness is assumed to be small and the relative water depth is assumed to be of order unity, which implies that this theory is valid for relatively deep water. In the cnoidal wave theory, both the square of the relative wave height and the relative water depth are assumed to be small, and the orders of these two quantities are assumed to the same. Therefore, cnoidal wave theory is applicable to relatively shallow water.
Isobe et al. (1982) made a detailed study of the ranges of validity of stokes wave and cnoidal wave theories. The applicable range of finite amplitude wave theory is based on Ursell parameter. Since the incident wave imposed in relatively deep water or offshore location, the Stokes wave is used here.
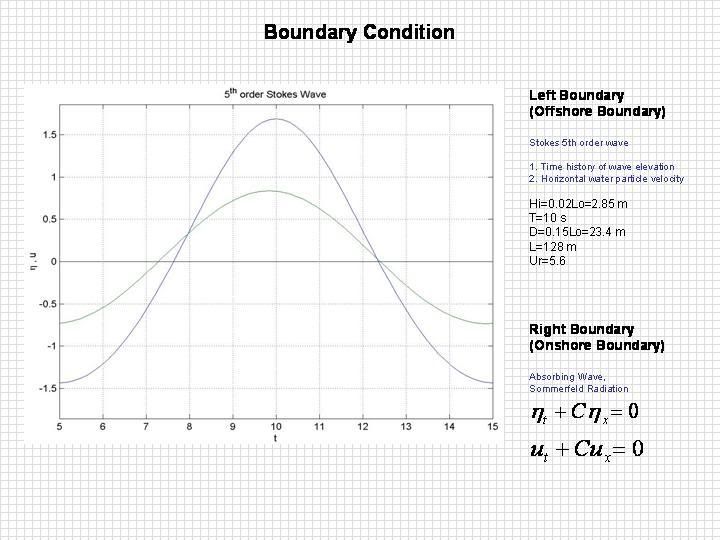
The wave profile drawn with a blue line and the horizontal water particle velocity drawn with a green line. The wave profile in the figure above exhibit a characteristic feature of finite amplitude waves, namely large, narrow crest and small, broad trough, as compared to linear wave theory. Since the numerical scheme is discretized in a staggered grid manner, the wave profile and horizontal water particle velocity is not plotted symmetrical to each other.
Absorbing boundary (onshore boundary)
1. Sommerfeld radiation or open boundary, which should absorb all energy arriving at the boundary from within the fluid domain. A perfect absorbing boundary should not allow wave reflection to occur.
2. Damping or sponge layer, which applied in order to reduce reflection in boundary as a short wave absorption.
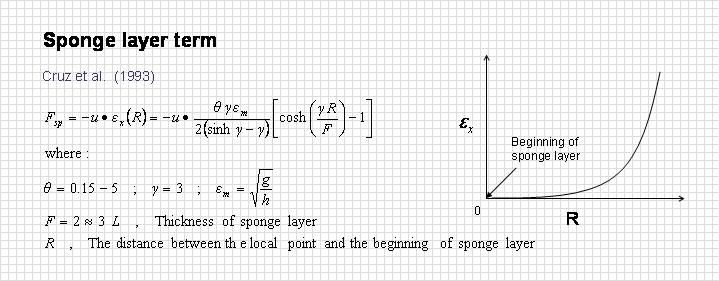
References can be found here.