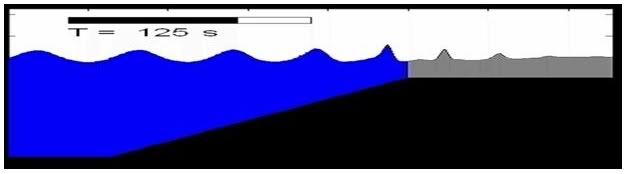
The waterline on a beach subjected to wave action is highly variable, and thus the physical domain in a nearshore Boussinesq model application changes in time. Although it is possible to utilize a time-dependent, shoreline-following grid system in order to resolve the fluid domain only up to the waterline, it is difficult to do so if the shoreline does not remain single valued or becomes multiply connected.
For this reason, it is more standard to employ techniques whereby the entire region which is potentially wetted is treated as an active part of the computational grid. One of the earliest methods along this line is the “slot” method of Tao (1984), in which deep, narrow, flooded slots are added to each grid row, extending down at least to the lowest elevation that will be experienced during shoreface rundown.
Kennedy et al (2000) employed the slot technique of Tao but modified it to better enforce mass conservation. Utilization of slot methods remains something of an art form to date. Slots which are too wide relative to the model grid spacing admit too much fluid before filling during runup, and cause both a reduction in amplitude and a phase lag in modeled runup events. At the other extreme, slots which are too narrow tend to induce a great deal of numerical noise, leading to the need for intermittent or even fairly frequent filtering of swash zone solutions.
The runup of waves on beaches has been studied extensively by scientist and non scientist. Although research has improved our understanding of many aspects of this phenomenon, there has been only limited success developing a general model which can theoretically predict the runup of arbitrary wave especially the wave break during approach to the shoreline. Even non-breaking waves are difficult to treat because the shoreline represents a moving boundary, which must be computed as part of the solution.
In a wave runup problem, it is not easy to express moving boundary for a wave front with the fixed coordinate system in the Eulerian description which is used for most of wave models with finite difference method. Moving shoreline is difficult to treat because it represents a moving boundary which must be computed as part of the solution.
Alternately, several moving boundary techniques where the occurrence of a shoreline is traced on a fixed grid have been proposed. In one such method, Lynett et al (2002) determine the position of the shoreline on a beach face by linearly extrapolating the surface and velocities from the two wetted grid points closest to shore. Derivatives at wetted grid points are then computed using the regular finite difference stencil including extrapolated values, eliminating the need for conditional application of off-centered difference stencils near shore. The time stepping solution is then only performed for the wetted grid points.
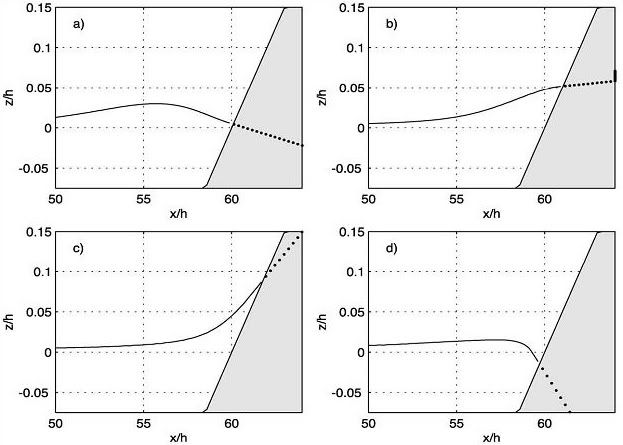
The moving boundary algorithm is conceptually simple, easy to implement, and can be employed by different numerical schemes (i.e., finite difference and finite element) utilizing depth-integrated Boussinesq equations. The moving boundary technique utilizes linear extrapolation through the wet–dry boundary and into the dry region, thereby allowing the real boundary location to exist in-between nodal points.
Although this method does not impose any apparent constraints on mass conservation at the shoreline, results for runup of regular and solitary waves are seen to be quite accurate, indicating that the method holds promise for general application.
References can be found here.