As waves propagate toward shore, a combination of shoaling, refraction, reflection, and diffraction effects modify the waveform. With further decrease in water depth, the wave height increases rapidly and finally waves break.
Wave breaking process is recognized as an irreversible transformation during which wave motion shifts from initially irrotational, simply-connected free surface dynamics to strong turbulence resulted from the intense vorticity generated by the folding of the free surface onto itself. Accompanying this special wave deformation, the dissipation of wave energy thus the decay of wave height is one of the principal characteristics of wave breaking.
The Boussinesq-type equations, which include the weak non-linearity and frequency dispersion provide an accurate description of wave transformation processes outside the surf zone. However, the Boussinesq equations do not automatically lead to wave breaking in shallow water nor to predict the wave in the surf zone. Then a natural step forward is an extension of the Boussinesq equations to cover the surf zone. The extension will require introduction of a wave breaking criterion and the introduction of energy dissipation.
One advantage of extending Boussinesq-type models to the surf zone is the ability to implicitly model interactions between hydrodynamics processes occurring at different time scale. Wave-induced currents and mean sea water level fluctuations are implicitly included in the wave propagation model and are derived from a time-average of the predicted velocities and surface wave elevation respectively, without having to explicitly calculate radiation stresses and separately solve a time-averaged hydrodynamic model.
Accordingly, there have been attempts to introduce wave breaking into Boussinesq models in order to model breaking phenomena such as wave height decay, wave-induced setup, and runup. The models essentially incorporate a dissipative term due to turbulence stresses or the presence of a surface roller into the momentum equation. The models differ on how they treat the onset of breaking and the rate of wave energy dissipation.
Simulation of wave breaking in Boussinesq models has been approached with a number of techniques, ranging from fairly ad-hoc additions of eddy viscosity formulations up to reasonably detailed calculations of the generation and transport of vorticity or turbulent kinetic energy under the breaking wave crest. Regardless of the formulation, each of the approaches can be thought of as a means for adding the breaking wave force term to the momentum equation.
At minimum, these terms must be scaled similarly in order to reproduce the correct amount of energy dissipation. They must also be localized in the region of the front face of the breaking wave, in order to provide the correct distribution of dissipation in the frequency domain and preserve the proper relative phasing of harmonic components in the wave. Beyond these requirements, the range of physical approaches taken has a great deal of variety.
Zelt (1991) used the Lagrangian finite-element Boussinesq wave model to study the breaking and runup of solitary waves. Wave dissipation due to turbulence generated by wave breaking is treated by an artificial viscosity term in the momentum equation. The horizontal velocity gradient is used as a breaking criterion to decide exactly when and where the dissipation becomes active.
Karambas and Koutitas (1992) extended the Boussinesq equations to cover the surf zone. The energy dissipation due to wave breaking was represented by including an eddy viscosity term in the depth-integrated momentum equation. The eddy viscosity coefficient is calculated from the numerical integration of the turbulent transport equation and the mixing length hypothesis. Crest elevation at breaking point with the wavelength in deep water was used as a breaking criterion.
Schaffer et al. (1994) used the concept of surface rollers to incorporate wave breaking in Boussinesq equations. The roller is considered as a volume of water being carried by the wave with wave celerity. The effect of the roller is induced in the vertical distribution of the horizontal velocity, which leads to an additional convective momentum term. The breaking criterion is related to the local slope of water surface and the thickness of the roller is determined from simple geometrical considerations.
Kabiling and Sato (1994) added a momentum mixing term using eddy viscosity to the momentum conservation equations to simulate the energy dissipation due to breaking. A breaking criterion using the ratio of the water particle velocity at the surface to the wave celerity was presented.
Nwogu (1996) extended the Boussinesq model to the surf zone by coupling the mass and momentum equations with one-equation model for the temporal and spatial evolution of the turbulent kinetic energy induced by wave breaking. The waves are assumed to start breaking when the horizontal component of the orbital velocity at the crest exceeds the phase velocity of the waves. The rate of wave energy dissipation, which is equal to the rate of production of turbulent kinetic energy, is assumed to be proportional to the vertical gradient of the horizontal water particle velocity at wave crest.
Svendsen (1996) describe a breaking wave model based on the classical assumptions for long, moderately nonlinear Boussinesq waves. The wave breaking is represented by including the vorticity generated by the breaking.
Kennedy (2000) used a momentum-conserving eddy viscosity technique to model breaking. This is somewhat like the eddy viscosity formulation Zelt (1991), but with extensions to provide a more realistic description of the initiation and cessation of wave breaking.
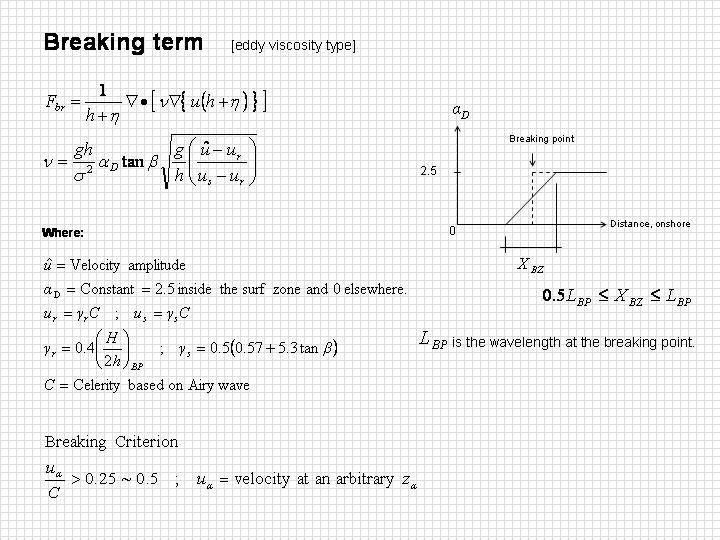
A time-dependent wave breaking model used by Sato and Kabiling (1994) is adopted and implemented as the wave breaking criterion and energy dissipation for numerical model. The models essentially incorporate a dissipative term due to turbulence stresses into the momentum equation. A time-dependent breaking model is also able to simulate the transition region after the onset of wave breaking, where there is a rapid decay in wave energy.
References can be found here.